Overfitting & The Problem Of Overfitting

Sometimes, the algorithm can run into a problem called overfitting which can cause it to perform poorly. To help us understand what overfitting is , let's take a look at a few examples. Let's use the example where we want to predict the price of a house given the size of the hous

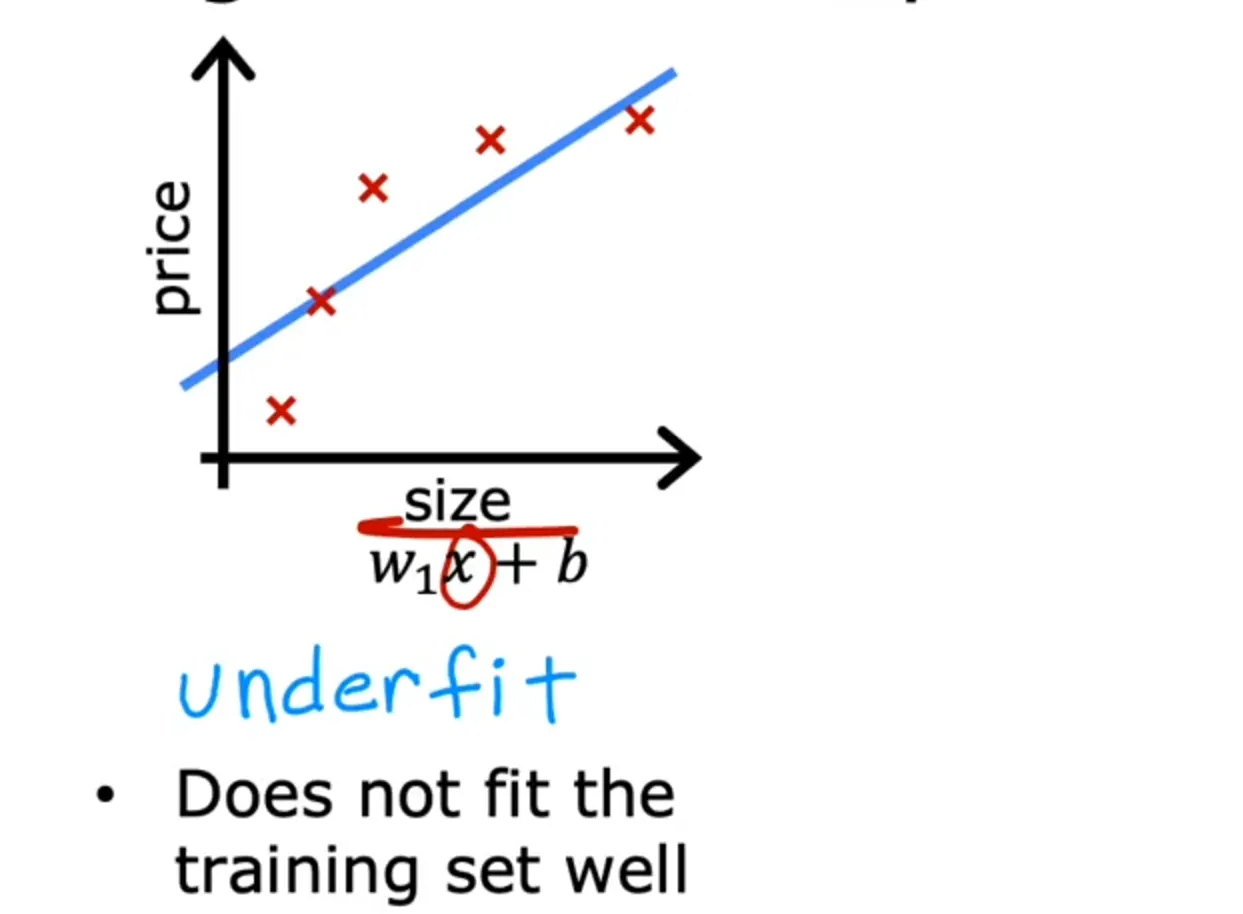
Assuming your dataset looks like the image above, one thing you could do is to fit a linear function to this data and if you do that, you get a straight line fit to the data but this isn't a very good model. Looking at the data, it seems pretty clear that as the size of the house increases, the price kind of flattens out. So this algorithm does not fit the training data very well. The technical term for this is that the model is underfitting the training data another term is the algorithm has a high bias — meaning it has not been able to fit the training data very well i.e. there is a pattern in the training data that the algorithm is unable to capture.

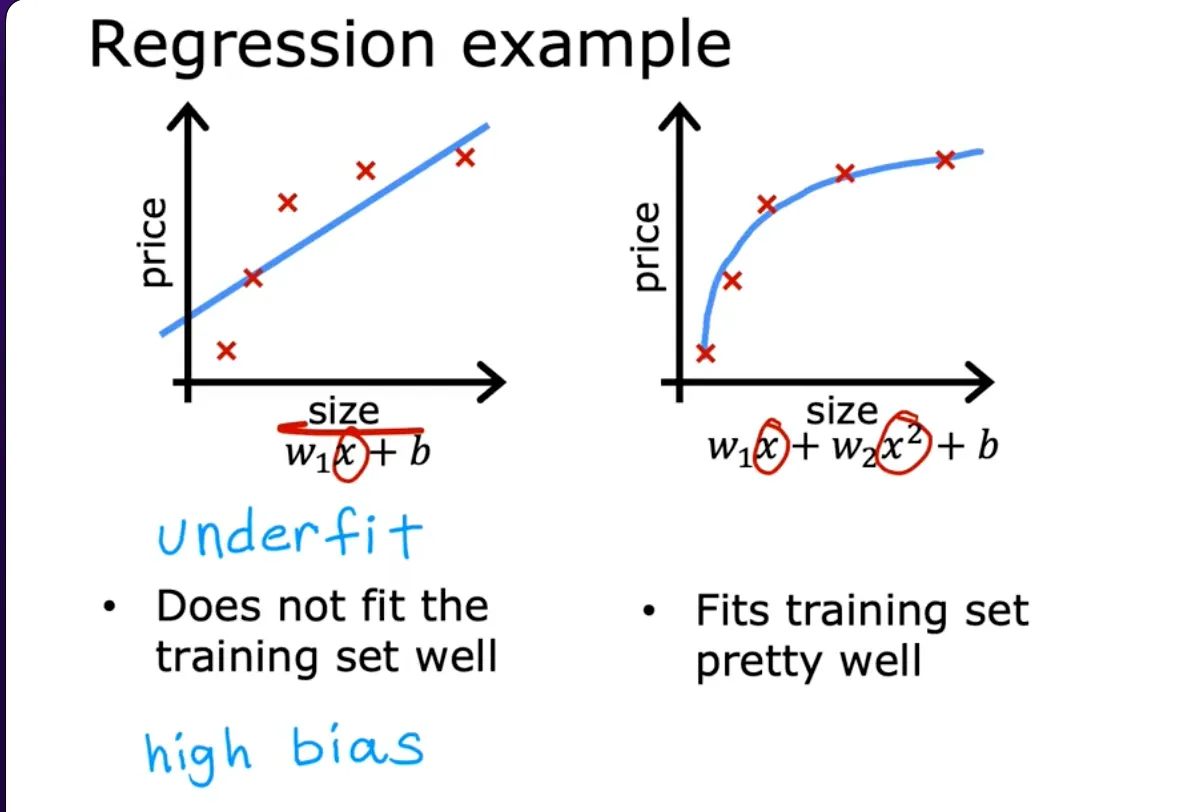
Now let’s look at a second variation of a model which is if you insert a quadratic function to the data with two features, x, and x², then when you fit the parameters W1 and W2, you can get a curve that fits the data somewhat better. This model would probably do quite well on that new house. The idea that you want your learning algorithm to do well, even on examples that are not on the training set, is called generalization. Technically we say that you want your learning algorithm to generalize well, which means it makes good predictions even on brand-new examples that it has never seen before.

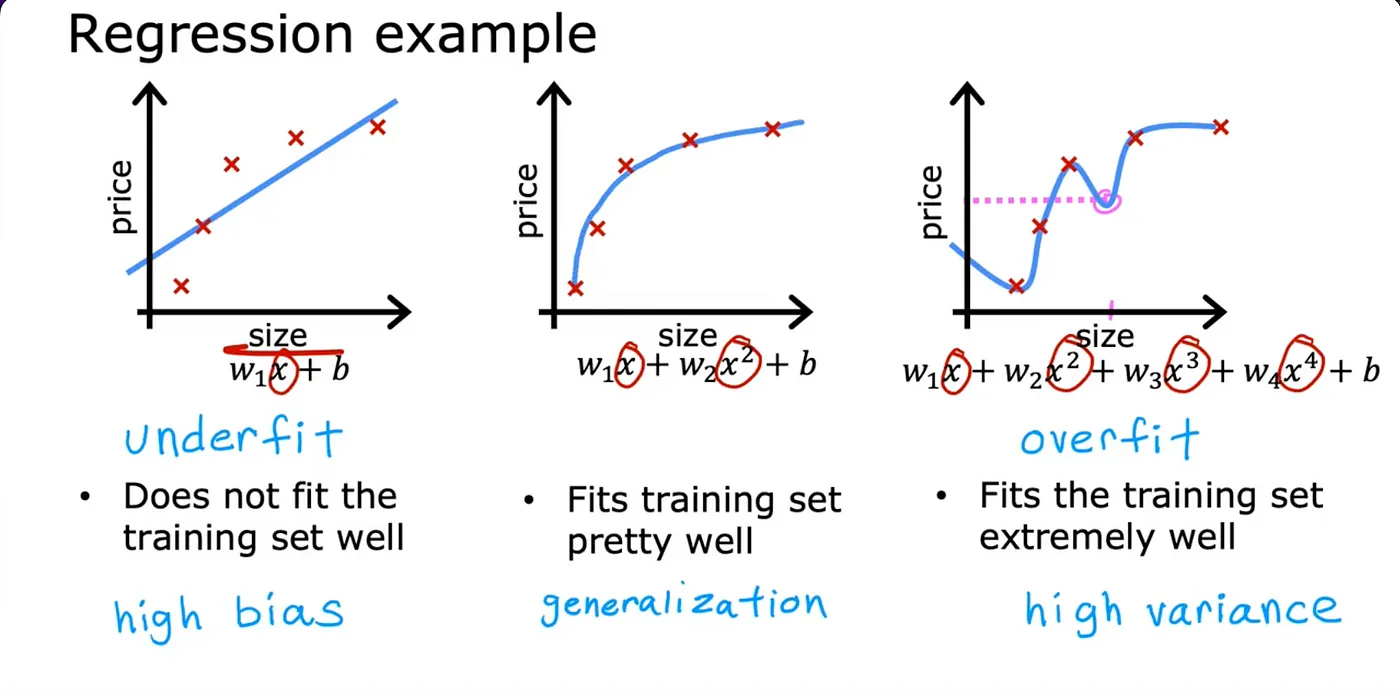
What if you were to fit a fourth-order polynomial to the data? With this fourth-order polynomial, you can actually fit the curve that passes through all five of the training examples exactly. This diagram seems to do an extremely good job fitting the training data because it passes through all the training data perfectly. In fact, you’d be able to choose parameters that will result in the cost function being exactly equal to zero because the errors are zero on all five training examples. We don’t think that this is a particularly good model for predicting housing prices. The technical term is that we’ll say this model has overfit the data, or this model has an overfitting problem. Because even though it fits the training set very well, it has fit the data almost too well, hence is an overfit. It does not look like this model will generalize to new examples that it has never seen before. Another term for this is that the algorithm has high variance. The intuition behind overfitting or high variance is that the algorithm is trying very hard to fit every single training example. You can say that the goal of machine learning is to find a model that hopefully is neither underfitting nor overfitting.

In other words, hopefully, a model that has neither high bias nor high variance. When I think about underfitting and overfitting, high bias and high variance, I am sometimes reminded of the children’s story of Goldilocks and the Three Bears in this children’s tale, a girl called Goldilocks visits the home of a bear family. There’s a bowl of porridge that’s too cold to taste and so that’s no good. There’s also a bowl of porridge that’s too hot to eat. That’s no good either. But there’s a bowl of porridge that is neither too cold nor too hot. The temperature is in the middle, which is just right to eat.